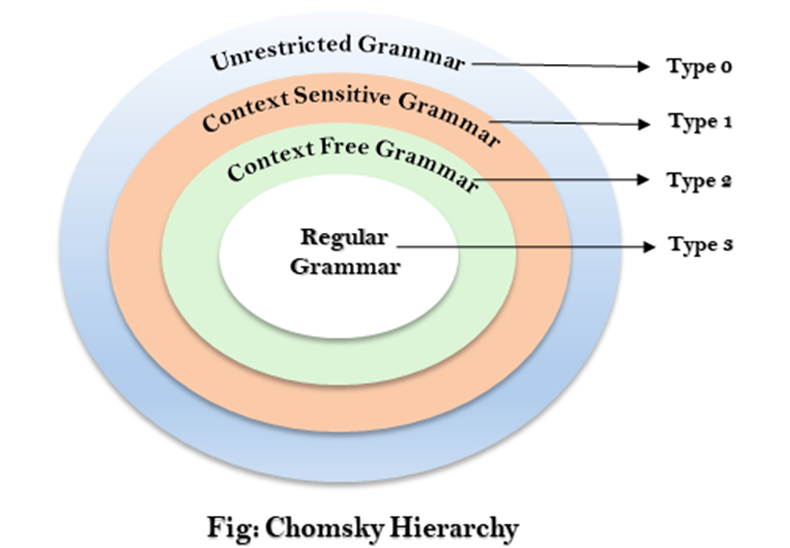
Chomsky Hierarchy

Chomsky Hierarchy

Chomsky Hierarchy represents the class of languages that are accepted by the different machine. The category of language in Chomsky's Hierarchy is as given below:

1. Type 0 known as Unrestricted Grammar.
2. Type 1 known as Context Sensitive Grammar.
3. Type 2 known as Context Free Grammar.
4. Type 3 Regular Grammar.

This is a hierarchy. Therefore every language of type 3 is also of type 2, 1 and 0. Similarly, every language of type 2 is also of type 1 and type 0, etc.

Type 0 Grammar:

Type 0 grammar is known as Unrestricted grammar. There is no restriction on the grammar rules of these types of languages. These languages can be efficiently modeled by Turing machines.

For example:

1.     bAa → aa  

2.     S → s  

Type 1 Grammar:

Type 1 grammar is known as Context Sensitive Grammar. The context sensitive grammar is used to represent context sensitive language. The context sensitive grammar follows the following rules:

• The context sensitive grammar may have more than one symbol on the left hand side of their production rules.
• The number of symbols on the left-hand side must not exceed the number of symbols on the right-hand side.
• The rule of the form A → ε is not allowed unless A is a start symbol. It does not occur on the right-hand side of any rule.
• The Type 1 grammar should be Type 0. In type 1, Production is in the form of V → T

Where the count of symbol in V is less than or equal to T.

For example:

1.     S → AT  

2.     T → xy  

3.     A → a  

Type 2 Grammar:

Type 2 Grammar is known as Context Free Grammar. Context free languages are the languages which can be represented by the context free grammar (CFG). Type 2 should be type 1. The production rule is of the form

1.     A → α  

Where A is any single non-terminal and is any combination of terminals and non-terminals.

For example:

1.     A → aBb  

2.     A → b  

3.     B → a  

Type 3 Grammar:

Type 3 Grammar is known as Regular Grammar. Regular languages are those languages which can be described using regular expressions. These languages can be modeled by NFA or DFA.

Type 3 is most restricted form of grammar. The Type 3 grammar should be Type 2 and Type 1. Type 3 should be in the form of

1.     V → T*V / T*  

For example:

1.     A → xy  

 

 

Pumping Lemma for L = {a | k is a prime number}

  L = {a | k is a prime number}

Let us assume L is regular.  

-> Clearly L is infinite (there are infinitely many prime numbers). From the pumping lemma, there exists a number n such that any string w of length greater than n has a “repeatable” substring generating more strings in the language L.

Let us consider the first prime number p >= n.

For example, 

if n was 50 we could use p = 53. 

From the pumping lemma the string of length p has a “repeatable” substring. We will assume that this substring is of length k >= 1.

Hence:

It should be relatively clear that p + k, p + 2k, etc., cannot all be prime but let us add k p times, then we must have:

so this would imply that (k + 1)p is prime, which it is not since it is divisible by both p and k + 1. Hence L is not regular. 

Pumping Lemma for Regular Languges

Pumping lemma used to show that language is not regular. 

What is pumping?

for regular expression

r = (a u b) (abb)* (bba u bbb), the string w= babbbbb pumps because we may decompose w into three sub strings.

w= b.  abb.  bbb

such that  b(abb)i bbb is represented by r, for every i>= 0.

in this DFA.,

the string aaabab= aa. aba.b pumps because of the cycle that the aba follows.

Suppose L is a regular Language., the there exists an integer k such that for all strings z belongs to L. , satisfying |z|>=k., we can write z= uvw where

|v| >= 1

|uv| <=k

u vi  w  belongs to L, for all i>=0.